Tervezz! Alkoss!
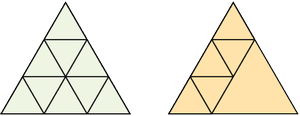
Vágj ki hat egyforma szabályos háromszöglapot kartonpapírból! Tervezz minél több síkidomot, amelyeket a hat háromszögből raksz össze! Ezeket rajzold le a füzetedbe! Mindig teljes oldalaknak kell illeszkedniük egymáshoz. Az így kapott síkidomokat el is nevezheted, ha emlékeztetnek valamire.
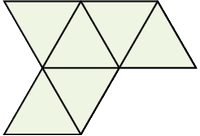
Egyet mi is építettünk. Ezt mi pisztolynak nevezzük!
A háromszögeket már csoportosítottuk a szögeik és az oldalaik alapján. Most szimmetriájuk alapján fogjuk vizsgálni őket.
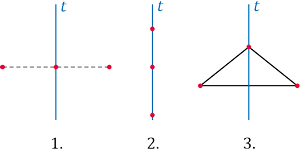
Három pont szimmetrikus helyzetei:
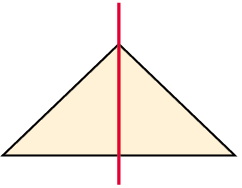
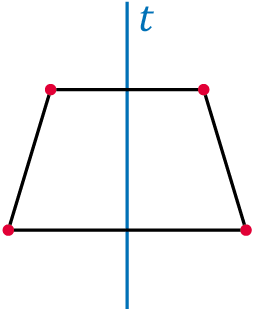
– A három pont egy egyenesen van, és közülük pontosan egy illeszkedik a tengelyre (1.)
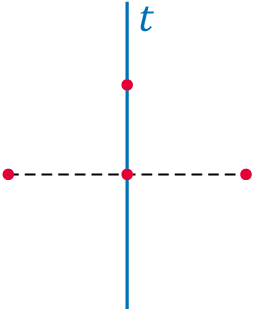
– A három pont illeszkedik a tengelyre (2.)
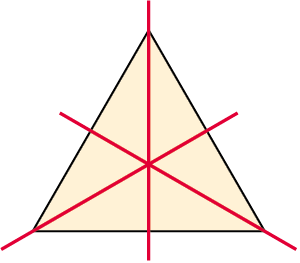
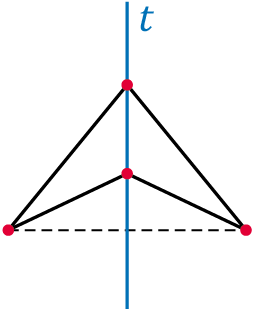
– A három pont nincs egy egyenesen, és közülük pontosan egy illeszkedik a tengelyre (3.)
Ha a három pont nincs egy egyenesen és szimmetrikus helyzetű, akkor ezeket összekötve tengelyesen szimmetrikus háromszöget, vagyis tengelyesen tükrös háromszöget kapunk.
Az eddigi ismereteink alapján:
Kiemeljük a mondatok lényegét:
a) Ha egy háromszög szimmetrikus, akkor van két egyenlő hosszú oldala (azaz egyenlő szárú).
Ha szimmetrikus, akkor egyenlő szárú.
b) Ha egy háromszög egyenlő szárú, akkor szimmetrikus.
Ha egyenlő szárú, akkor szimmetrikus.
Gondolkodjatok el azon, miért nem lehet pontosan két szimmetriatengelye egy háromszögnek!
Egy háromszög pontosan akkor szimmetrikus, ha egyenlő szárú.
Az egyenlő oldalú háromszögeknek három szimmetriatengelye van.
A háromszögeket csoportosíthatjuk a szimmetriatengelyek száma szerint:
– nincs tengelye;
– egy tengelye van;
– három tengelye van.
1. példa
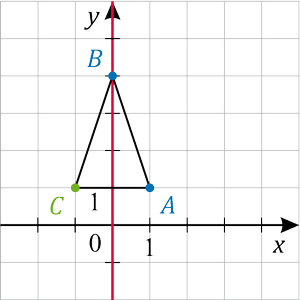
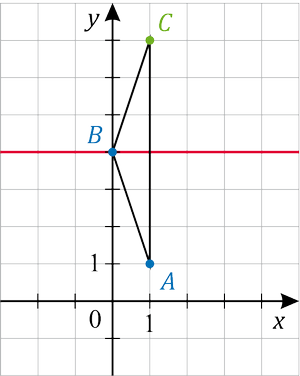
Szimmetrikus háromszöget szeretnénk rajzolni a koordináta-rendszerben. A háromszög két csúcsa: A(1; 1), B(0; 4). Adjuk meg a C csúcs koordinátáit, ha a háromszög szimmetriatengelye az
-
y tengely;
-
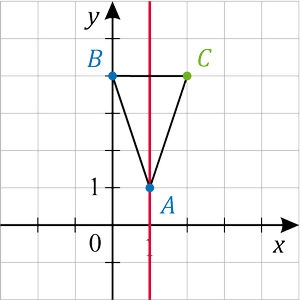
y tengellyel párhuzamos egyenes;
-
x tengellyel párhuzamos egyenes;
-
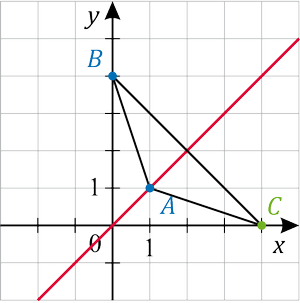
első negyed szögfelezője!
Megoldás
Páros munka
Rajzoljatok közösen szimmetrikus háromszöget! Húzzatok egy egyenest, ez lesz a tükörtengely! Egyikőtök csak az egyik, másikótok csak a másik oldalára rajzolhat a tengelynek. Végül egy tükrös háromszöget kell kapnotok. Először rajzoljatok egymást váltogatva egy-egy háromszöget, aztán próbáljátok meg úgy is, hogy egyszerre rajzoltok!
Játszhatjátok ugyanezt a játékot úgy is, hogy szimmetrikus négyszögnek kell keletkeznie.
Vizsgáljuk meg négy pont szimmetrikus helyzeteit!
-
A négy pont a tengelyre illeszkedik.
-
Két pont illeszkedik a tengelyre, a további kettő egymás tükörképe.
-
Egyik pont sem illeszkedik a tengelyre, kettő-kettő egymás tükörképe.
Ha a négy pont közül semelyik három nincs egy egyenesen és szimmetrikus helyzetűek, akkor a négy pontot összekötve tengelyesen szimmetrikus négyszöget, vagyis tengelyesen tükrös négyszöget kapunk.
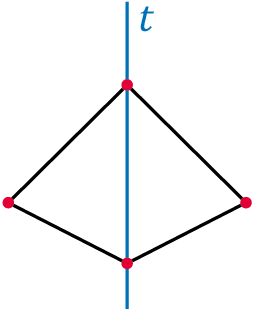
Deltoidot kapunk, ha két pont illeszkedik a tengelyre (2. a) és 2. c) ábra).
Ha egyik pont sem illeszkedik a tengelyre, akkor trapézt kapunk. Ezt a trapézt nevezzük szimmetrikus trapéznak (3. a) ábra).
A szabályos sokszögeknek nem csak egy szimmetriatengelyük van.
2. példa
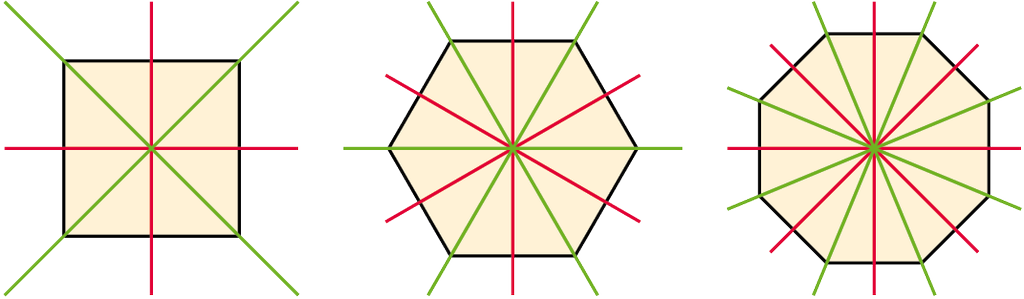
Rajzoljuk meg a szabályos négyszög, hatszög, nyolcszög szimmetriatengelyeit! Adjuk meg a tengelyek számát!
Megoldás
3. példa
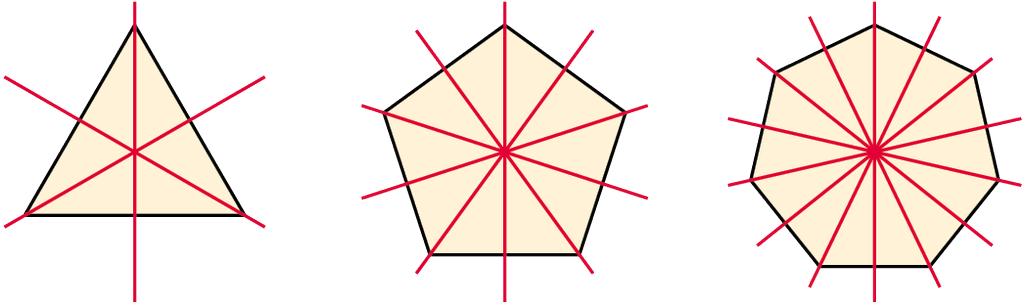
Rajzoljuk meg a szabályos háromszög, ötszög, hétszög szimmetriatengelyeit! Adjuk meg a tengelyek számát!
Megoldás
A sokszögek között is vannak tengelyesen szimmetrikusak.
4. példa
Rajzoljunk néhány tengelyesen szimmetrikus sokszöget a tengelyével! Az ábrák lehetőleg szemléltessenek valamilyen hétköznapi dolgot!
Megoldás
Játék
Keressetek 1 perc alatt a koordináta-rendszerben olyan C rácspontokat, amelyek az A(1; 4) és a B(4; 2) pontokkal szimmetrikus háromszöget alkotnak! Az idő leteltekor sorban egyesével olvassátok fel a talált pontok koordinátáit! Amit többen is írtak, azt a pontot mindenki áthúzza a füzetében. A győztes az lesz, akinek a legtöbb nem áthúzott pontja marad!
Feladatok
-
Egy szimmetrikus háromszög egyik oldalának hossza 4 cm, a másik oldalának hossza pedig 3 cm. Mekkora lehet a háromszög harmadik oldalának hossza? Szerkeszd meg a füzetedbe! -
Az egyenlő szárú háromszög két oldalának hossza 5 cm és 2 cm. Mekkora lehet a háromszög harmadik oldalának hossza? Szerkeszd meg a füzetedbe!
-
Megadunk a koordináta-rendszerben hat pontot: A(1; 2), B(2; 6), C(4; 1), D(4; –1), E(7; 4), F(7; –2). Válassz közülük hármat úgy, hogy azok egy egyenlő szárú háromszög csúcsai legyenek! Hány megfelelő ponthármast találtál?
-
Mekkorák lehetnek a szimmetrikus háromszög hiányzó szögei, ha az egyik szöge 56°-os? -
Az ábrán látható szabályos háromszöget kilenc, illetve hat szabályos háromszögre vágtuk. Hogyan vágnál szét egy szabályos háromszöget nyolc (nem feltétlenül egyforma) szabályos háromszögre?
-
Készíts négyzetek és egy téglalap felhasználásával szimmetrikus ábrát!
-
Készíts körvonalak segítségével szimmetrikus ábrát!
-
-
Rajzolj olyan közlekedési táblákat, amelyek tengelyesen szimmetrikusak!
Háromszögek szimmetriái
